Gallery
This page collects screenshots from various simulations that have used GLVis visualization. Additional images can be found in the MFEM Gallery.
The GLVis logo is derived from the Metatron model at bathsheba.com. Shown is the magnitude of the projection of a smooth vector field using 4th order Nedelec elements on a second order curved tetrahedral mesh (based on MFEM's Example 3).
Axisymmetric problem with revolved 2D mesh and solution, plus coloring grid functions emphasizing mesh elements. See also the video.
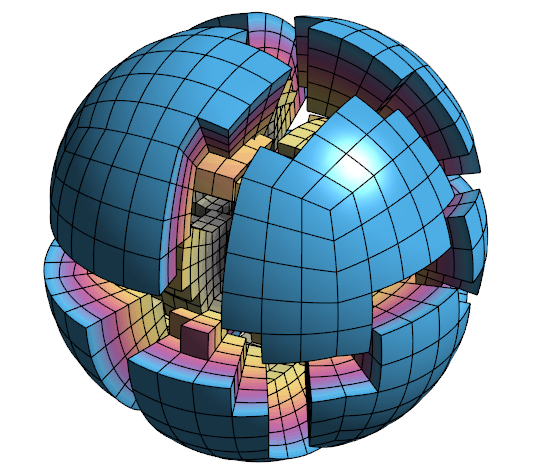
Unstructured parallel decomposition of a fourth order NURBS mesh of the unit ball obtained in the solution of MFEM's parallel Example 1 on 16 processors.
Quadrature data visualization on a low-order-refined (LOR) mesh. Several different visualization options are available via key 'Q'.
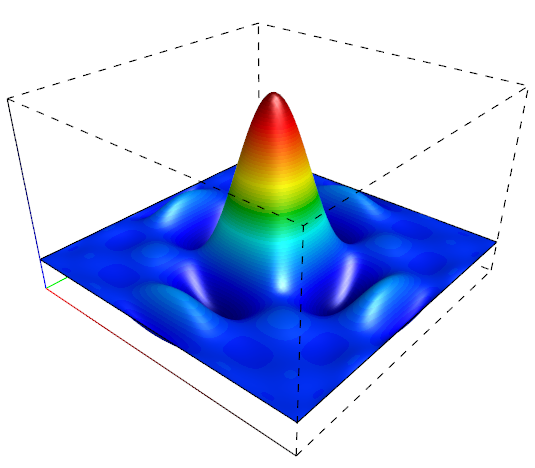
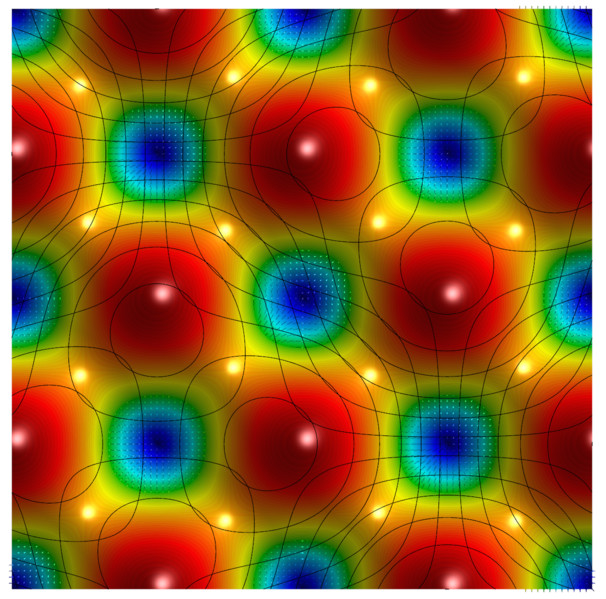
One of the eight order (Q8) basis functions on the reference square. The sub-refinement in GLVis (key 'i') allows for the correct visualization of such high-order functions.
GLVis model opened in augmented reality with the glTF model viewer.
Curvilinear 8th order mesh from a triple-point shock simulation in the MFEM-based BLAST shock hydrodynamics code. Click for a movie of the evolution of the processor partitioning from a high-resolution parallel run of the problem produced with a GLVis script.
Raytraced glTF model in Blender which was exported from GLVis with the 'G' key. The mesh faces have been cut with 'Ctrl+F3'
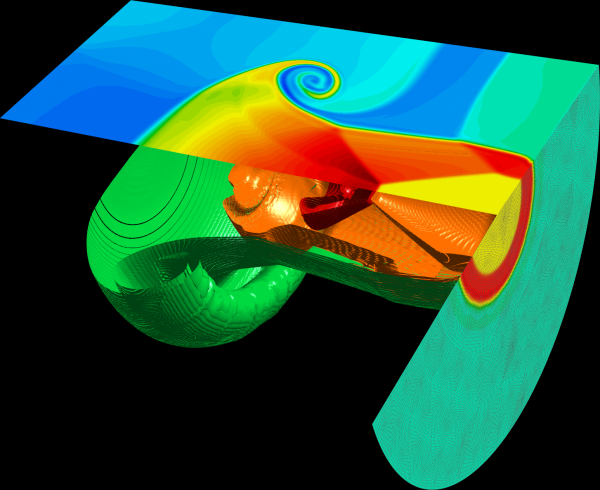
3D Arbitrary Lagrangian-Eulerian (ALE) simulation of a shock-triple point interaction with Q2-Q1 elements in the MFEM-based BLAST shock hydrodynamics code. Shown are the cutting plane and level surface capabilities of GLVis.
Parallel partitioning of a non-conforming adaptively refined mesh between 2048 processors based on splitting a space-filling (Hilbert) curve.
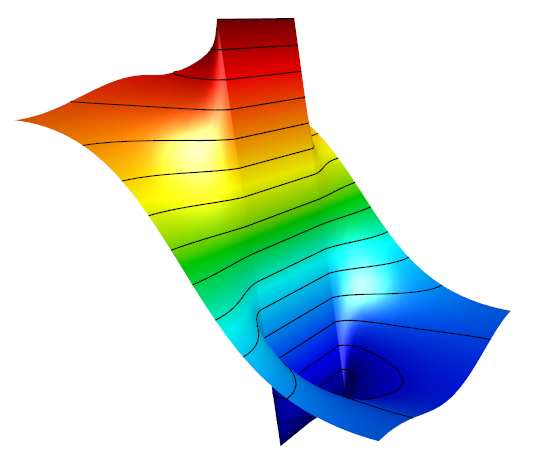
Level lines in 2D. Simulation with MFEM.
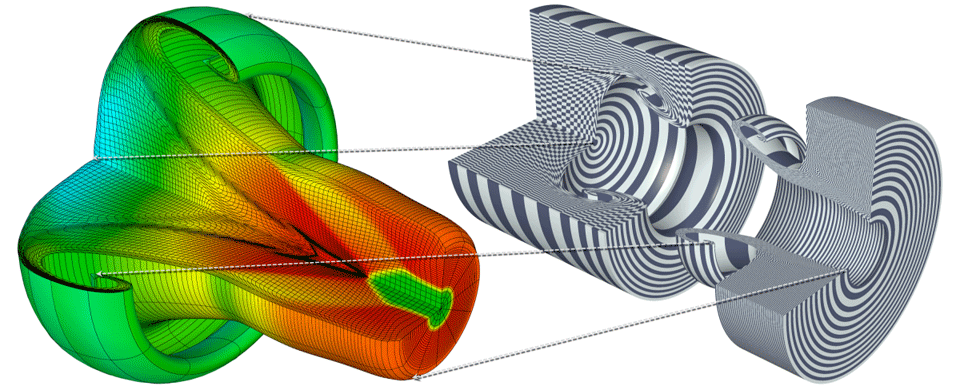
The SIAM CSE13 logo illustrates the decomposition of a hexahedral zone in tetrahedral "sides". This and related images can be found in this paper.
The vector field solution of grad-div problem on a periodic mesh computed with hybridized 3rd order Raviart-Thomas elements. Lines correspond to backward Cartesian displacements (key 'd' in GLVis).
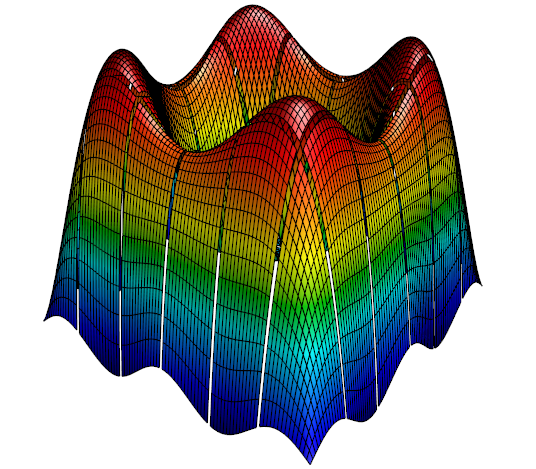
Stitched parallel results from hypre's Example 4 on 36 processors.
The solution of the Laplace problem on a 3D NURBS mesh. Shown are the solution values in a cutting plane and one of the internal boundaries.
Locally refined grid in 2D. Simulation with MFEM.